Iron Chromium Nickel Copper Molybdenum Niobium Alloy

See more Chromium products. Chromium (atomic symbol: Cr, atomic number: 24) is a Block D, Group 6, Period 4 element with an atomic weight of 51.9961. The number of electrons in each of Chromium's shells is 2, 8, 13, 1 and its electron configuration is [Ar] 3d⁵ 4s¹. Louis Nicolas Vauquelin first discovered chromium in 1797 and first isolated it the following year. The chromium atom has a radius of 128 pm and a Van der Waals radius of 189 pm. In its elemental form, chromium has a lustrous steel-gray appearance. Chromium is the hardest metallic element in the periodic table and the only element that exhibits antiferromagnetic ordering at room temperature, above which it transforms into a paramagnetic solid. The most common source of chromium is chromite ore (FeCr₂O₄). Due to its various colorful compounds, Chromium was named after the Greek word 'chroma.' meaning color.

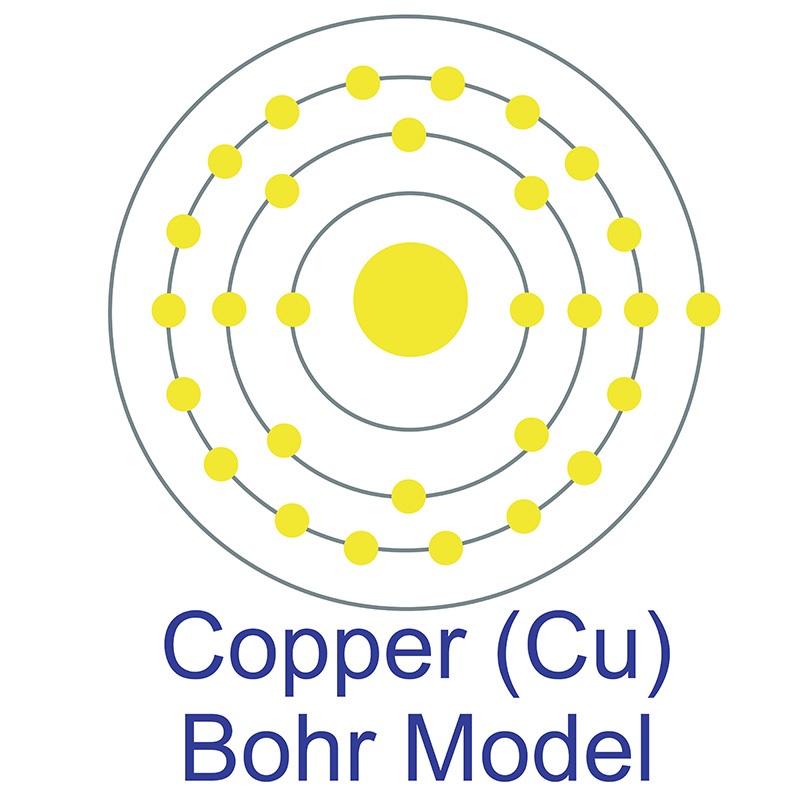See more Copper products. Copper (atomic symbol: Cu, atomic number: 29) is a Block D, Group 11, Period 4 element with an atomic weight of 63.546. The number of electrons in each of copper's shells is 2, 8, 18, 1 and its electron configuration is [Ar]3d¹⁰ 4s¹. The copper atom has a radius of 128 pm and a Van der Waals radius of 186 pm. Copper was first discovered by Early Man prior to 9000 BC. In its elemental form, copper has a reddish-orange metallic and lustrous appearance. Of all pure metals, only silver has a higher electrical conductivity. The origin of the word copper comes from the Latin word 'cuprium' which translates as "metal of Cyprus," as the Mediterranean island of Cyprus was known as an ancient source of mined copper..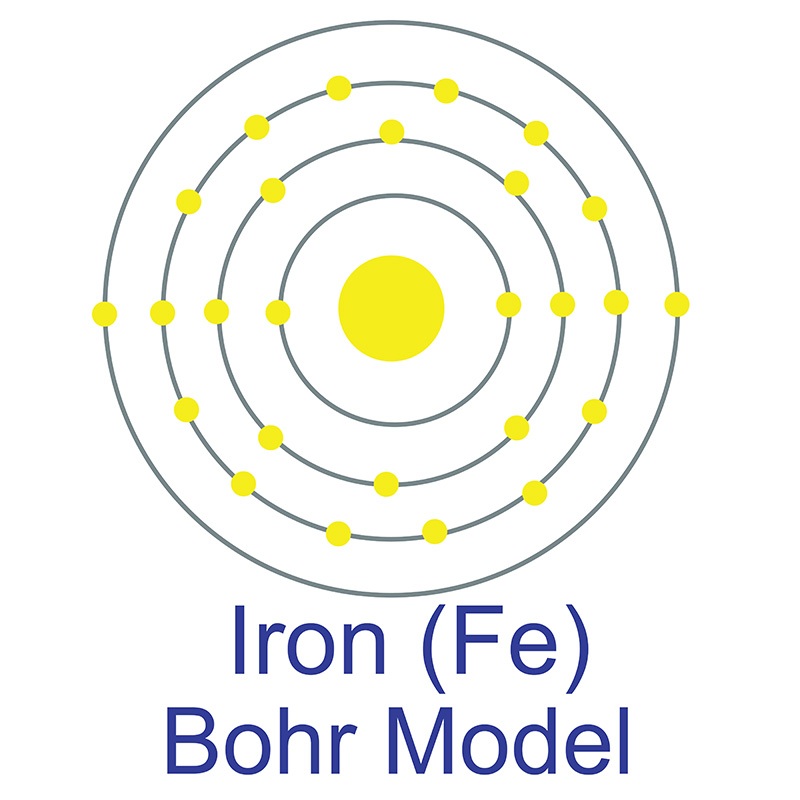

See more Iron products. Iron (atomic symbol: Fe, atomic number: 26) is a Block D, Group 8, Period 4 element with an atomic weight of 55.845. The number of electrons in each of Iron's shells is 2, 8, 14, 2 and its electron configuration is [Ar] 3d⁶ 4s². The iron atom has a radius of 126 pm and a Van der Waals radius of 194 pm. Iron was discovered by humans before 5000 BC. In its elemental form, iron has a lustrous grayish metallic appearance. Iron is the fourth most common element in the Earth's crust and the most common element by mass forming the earth as a whole. Iron is rarely found as a free element, since it tends to oxidize easily; it is usually found in minerals such as magnetite, hematite, goethite, limonite, or siderite. Though pure iron is typically soft, the addition of carbon creates the alloy known as steel, which is significantly stronger.

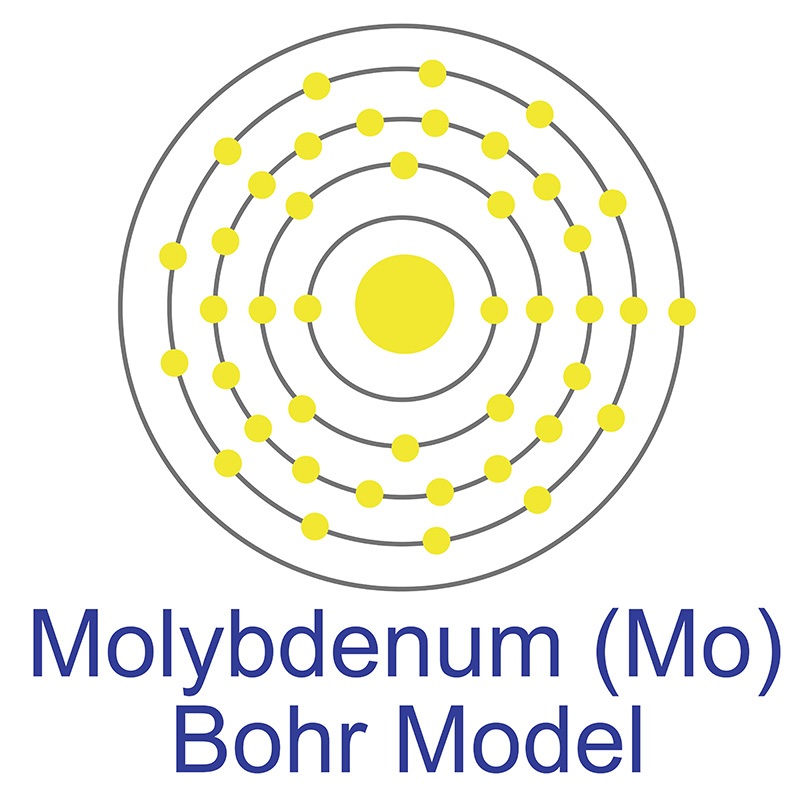See more Molybdenum products. Molybdenum (atomic symbol: Mo, atomic number: 42) is a Block D, Group 6, Period 5 element with an atomic weight of 95.96. The number of electrons in each of molybdenum's shells is [2, 8, 18, 13, 1] and its electron configuration is [Kr] 4d⁵ 5s¹. The molybdenum atom has a radius of 139 pm and a Van der Waals radius of 209 pm. In its elemental form, molybdenum has a gray metallic appearance. Molybdenum was discovered by Carl Wilhelm in 1778 and first isolated by Peter Jacob Hjelm in 1781. Molybdenum is the 54th most abundant element in the earth's crust. It has the third highest melting point of any element, exceeded only by 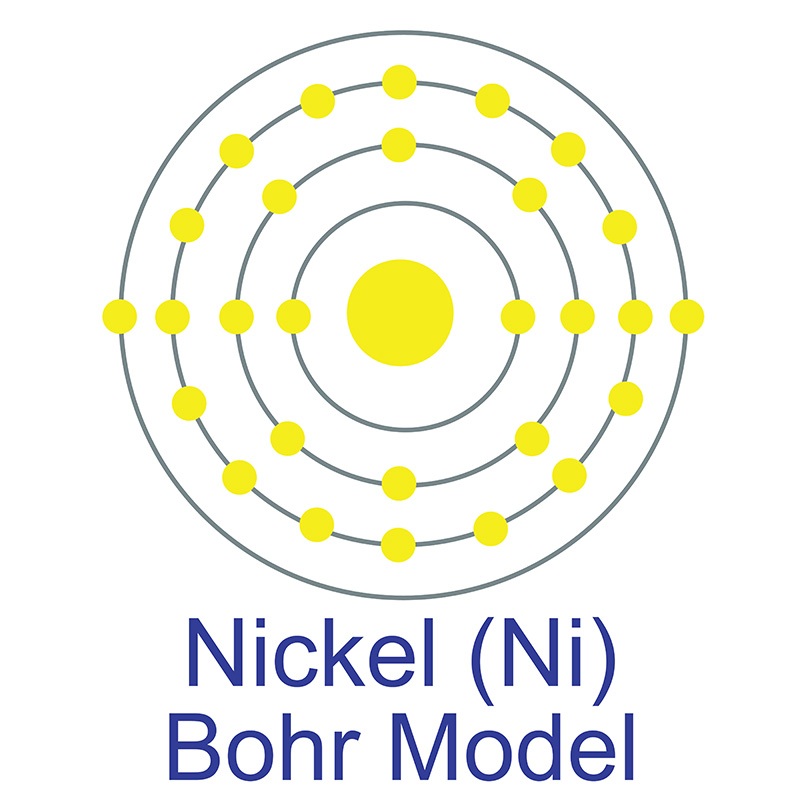tungsten and tantalum. Molybdenum does not occur naturally as a free metal, it is found in various oxidation states in minerals. The primary commercial source of molybdenum is molybdenite, although it is also recovered as a byproduct of copper and tungsten mining. The origin of the name Molybdenum comes from the Greek word molubdos meaning lead.

See more Nickel products. Nickel (atomic symbol: Ni, atomic number: 28) is a Block D, Group 4, Period 4 element with an atomic weight of 58.6934. The number of electrons in each of nickel's shells is [2, 8, 16, 2] and its electron configuration is [Ar]3d⁸ 4s². Nickel was first discovered by Alex Constedt in 1751. The nickel atom has a radius of 124 pm and a Van der Waals radius of 184 pm. In its elemental form, nickel has a lustrous metallic silver appearance. Nickel is a hard and ductile transition metal that is considered corrosion-resistant because of its slow rate of oxidation. It is one of four elements that are ferromagnetic and is used in the production of various type of magnets for commercial use. Nickel is sometimes found free in nature but is more commonly found in ores. The bulk of mined nickel comes from laterite and magmatic sulfide ores. The name originates from the German word kupfernickel, which means "false copper" from the illusory copper color of the ore.

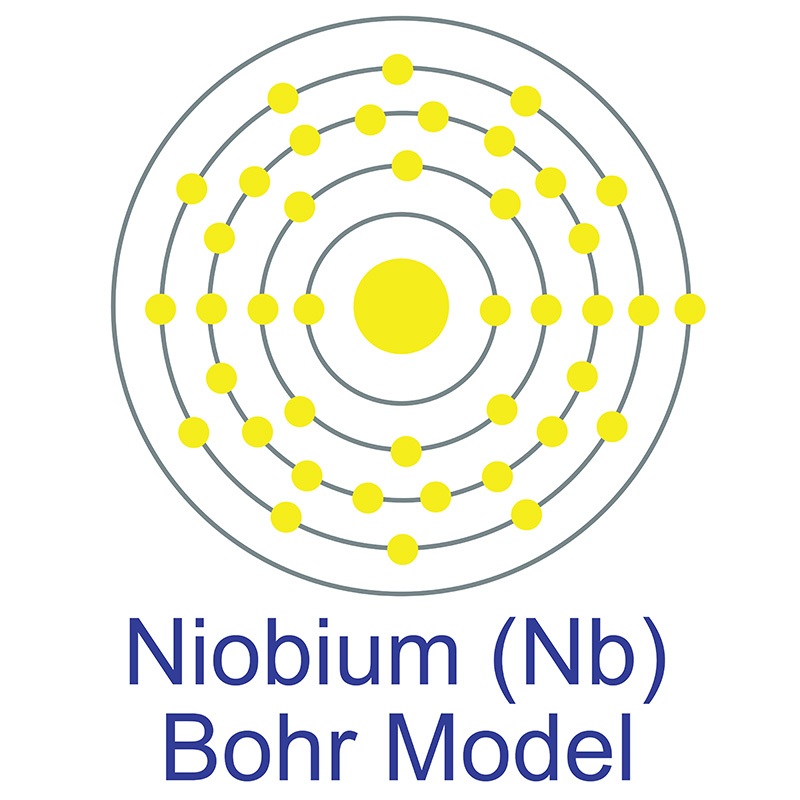See more Niobium products. Niobium (atomic symbol: Nb, atomic number: 41) is a Block D, Group 5, Period 5 element with an atomic weight of 92.90638. The number of electrons in each of niobium's shells is 2, 8, 18, 12, 1 and its electron configuration is [Kr] 4d⁴ 5s¹. The niobium atom has a radius of 146 pm and a Van der Waals radius of 207 pm. Niobium was discovered by Charles Hatchett in 1801 and first isolated by Christian Wilhelm Blomstrand in 1864. In its elemental form, niobium has a gray metallic appearance. Niobium has the largest magnetic penetration depth of any element and is one of three elemental type-II superconductors (along with vanadium and technetium). Niobium is found in the minerals pyrochlore, its main commercial source, and columbite. The word Niobium originates from Niobe, daughter of mythical Greek king Tantalus.